문제 설명
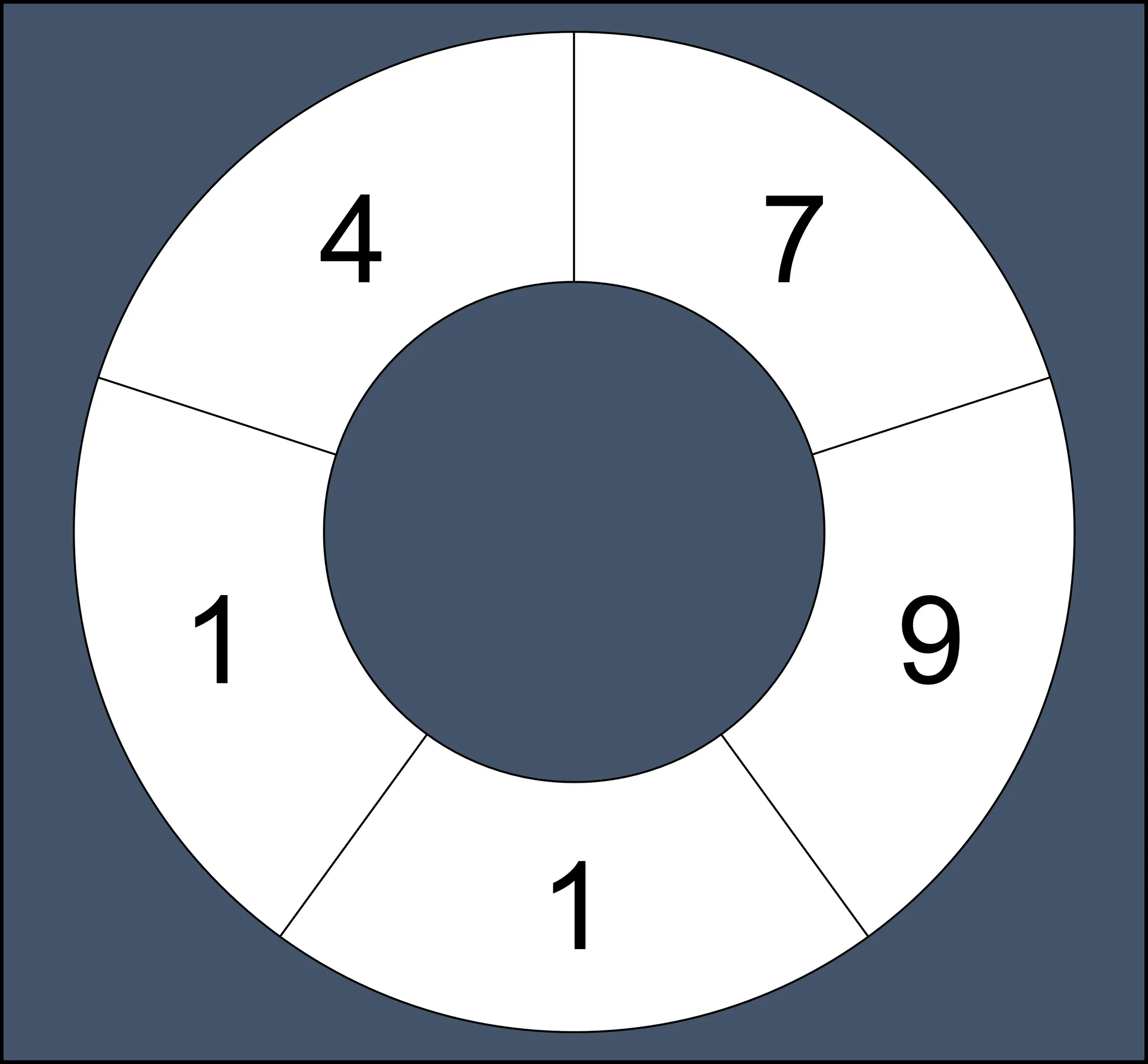
철호는 수열을 가지고 놀기 좋아합니다. 어느 날 철호는 어떤 자연수로 이루어진 원형 수열의 연속하는 부분 수열의 합으로 만들 수 있는 수가 모두 몇 가지인지 알아보고 싶어졌습니다. 원형 수열이란 일반적인 수열에서 처음과 끝이 연결된 형태의 수열을 말합니다. 예를 들어 수열 [7, 9, 1, 1, 4] 로 원형 수열을 만들면 다음과 같습니다.
원형 수열은 처음과 끝이 연결되어 끊기는 부분이 없기 때문에 연속하는 부분 수열도 일반적인 수열보다 많아집니다.
원형 수열의 모든 원소
elements
Plain Text
복사
가 순서대로 주어질 때, 원형 수열의 연속 부분 수열 합으로 만들 수 있는 수의 개수를 return 하도록 solution 함수를 완성해주세요.
제한사항
•
3 ≤ elements의 길이 ≤ 1,000
•
1 ≤ elements의 원소 ≤ 1,000
입출력 예
elements | result |
[7,9,1,1,4] | 18 |
입출력 예 설명
입출력 예 #1길이가 1인 연속 부분 수열로부터 [1, 4, 7, 9] 네 가지의 합이 나올 수 있습니다.길이가 2인 연속 부분 수열로부터 [2, 5, 10, 11, 16] 다섯 가지의 합이 나올 수 있습니다.길이가 3인 연속 부분 수열로부터 [6, 11, 12, 17, 20] 다섯 가지의 합이 나올 수 있습니다.길이가 4인 연속 부분 수열로부터 [13, 15, 18, 21] 네 가지의 합이 나올 수 있습니다.길이가 5인 연속 부분 수열로부터 [22] 한 가지의 합이 나올 수 있습니다.이들 중 중복되는 값을 제외하면 다음과 같은 18가지의 수들을 얻습니다.[1, 2, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 20, 21, 22]
나의 풀이
import java.util.*;
class Solution {
public int solution(int[] elements) {
Set<Integer> set = new HashSet<>();
// 부분수열(원소)의 길이 'len'
for (int len = 1; len <= elements.length; len++) {
// 시작점 index 'start'
for (int start = 0; start < elements.length; start++) {
int sum = 0;
// 'len'개 만큼 합함
for (int k = 0; k < len; k++) {
sum += elements[(start + k) % elements.length];
}
set.add(sum);
}
}
return set.size();
}
}
Java
복사
Remark
•
풀이 아이디어
◦
주석에 있는 것처럼 매우 정직하게 풀이함(시간복잡도 )
◦
덕분에 시간이 매우 오래 걸렸는데, 최적화를 할 수 없을까?
▪
진행하면서 sum을 초기화하지 않고 제일 왼쪽 값을 빼고 오른쪽 값만 더해주는 식으로 하면 훨씬 효율적일 것 같다는 생각이 듦(시간복잡도 )
import java.util.*;
class Solution {
public int solution(int[] elements) {
Set<Integer> set = new HashSet<>();
// 원소의 개수(길이) 'len'
for (int len = 1; len <= elements.length; len++) {
int sum = 0;
// 최초 1회는 sum을 초기화
for (int i = 0; i < len; i++) {
sum += elements[i];
}
set.add(sum);
// 시작점 index 'start'
for (int start = 1; start < elements.length; start++) {
// 부분수열 바로 왼쪽 값을 빼주고 바로 오른쪽 값을 더하는 것을 반복
// 빼기를 하면 index가 -가 되니, (배열 길이 - 1) 만큼을 더함
sum -= elements[(start + elements.length -1) % elements.length];
sum += elements[(start + len - 1) % elements.length];
set.add(sum);
}
}
return set.size();
}
}
Java
복사
•
매우 빨라짐