문제 설명
XX게임에는 피로도 시스템(0 이상의 정수로 표현합니다)이 있으며, 일정 피로도를 사용해서 던전을 탐험할 수 있습니다. 이때, 각 던전마다 탐험을 시작하기 위해 필요한 "최소 필요 피로도"와 던전 탐험을 마쳤을 때 소모되는 "소모 피로도"가 있습니다. "최소 필요 피로도"는 해당 던전을 탐험하기 위해 가지고 있어야 하는 최소한의 피로도를 나타내며, "소모 피로도"는 던전을 탐험한 후 소모되는 피로도를 나타냅니다. 예를 들어 "최소 필요 피로도"가 80, "소모 피로도"가 20인 던전을 탐험하기 위해서는 유저의 현재 남은 피로도는 80 이상 이어야 하며, 던전을 탐험한 후에는 피로도 20이 소모됩니다.
이 게임에는 하루에 한 번씩 탐험할 수 있는 던전이 여러개 있는데, 한 유저가 오늘 이 던전들을 최대한 많이 탐험하려 합니다. 유저의 현재 피로도 k와 각 던전별 "최소 필요 피로도", "소모 피로도"가 담긴 2차원 배열 dungeons 가 매개변수로 주어질 때, 유저가 탐험할수 있는 최대 던전 수를 return 하도록 solution 함수를 완성해주세요.
제한사항
•
k는 1 이상 5,000 이하인 자연수입니다.
•
dungeons의 세로(행) 길이(즉, 던전의 개수)는 1 이상 8 이하입니다.
◦
dungeons의 가로(열) 길이는 2 입니다.
◦
dungeons의 각 행은 각 던전의 ["최소 필요 피로도", "소모 피로도"] 입니다.
◦
"최소 필요 피로도"는 항상 "소모 피로도"보다 크거나 같습니다.
◦
"최소 필요 피로도"와 "소모 피로도"는 1 이상 1,000 이하인 자연수입니다.
◦
서로 다른 던전의 ["최소 필요 피로도", "소모 피로도"]가 서로 같을 수 있습니다.
입출력 예
k | dungeons | result |
80 | [[80,20],[50,40],[30,10]] | 3 |
입출력 예 설명
현재 피로도는 80입니다.
만약, 첫 번째 → 두 번째 → 세 번째 던전 순서로 탐험한다면
•
현재 피로도는 80이며, 첫 번째 던전을 돌기위해 필요한 "최소 필요 피로도" 또한 80이므로, 첫 번째 던전을 탐험할 수 있습니다. 첫 번째 던전의 "소모 피로도"는 20이므로, 던전을 탐험한 후 남은 피로도는 60입니다.
•
남은 피로도는 60이며, 두 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 50이므로, 두 번째 던전을 탐험할 수 있습니다. 두 번째 던전의 "소모 피로도"는 40이므로, 던전을 탐험한 후 남은 피로도는 20입니다.
•
남은 피로도는 20이며, 세 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 30입니다. 따라서 세 번째 던전은 탐험할 수 없습니다.
만약, 첫 번째 → 세 번째 → 두 번째 던전 순서로 탐험한다면
•
현재 피로도는 80이며, 첫 번째 던전을 돌기위해 필요한 "최소 필요 피로도" 또한 80이므로, 첫 번째 던전을 탐험할 수 있습니다. 첫 번째 던전의 "소모 피로도"는 20이므로, 던전을 탐험한 후 남은 피로도는 60입니다.
•
남은 피로도는 60이며, 세 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 30이므로, 세 번째 던전을 탐험할 수 있습니다. 세 번째 던전의 "소모 피로도"는 10이므로, 던전을 탐험한 후 남은 피로도는 50입니다.
•
남은 피로도는 50이며, 두 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 50이므로, 두 번째 던전을 탐험할 수 있습니다. 두 번째 던전의 "소모 피로도"는 40이므로, 던전을 탐험한 후 남은 피로도는 10입니다.
따라서 이 경우 세 던전을 모두 탐험할 수 있으며, 유저가 탐험할 수 있는 최대 던전 수는 3입니다.
※ 공지 - 2022년 2월 25일 테스트케이스가 추가되었습니다.
나의 풀이
class Solution {
static int[][] dgs;
static int max = 0;
public int solution(int hp, int[][] dungeons) {
dgs = dungeons;
search(hp, new boolean[dgs.length]);
return max;
}
void search(int hp, boolean[] isVisited) {
for (int i = 0; i < dgs.length; i++) {
int requiredHp = dgs[i][0];
int costHp = dgs[i][1];
if (!isVisited[i] && hp >= requiredHp) {
boolean[] temp = isVisited.clone();
temp[i] = true;
search(hp - costHp, temp);
}
}
int visited = 0;
for (boolean b : isVisited) {
if (b) visited++;
}
if (visited > max) {
max = visited;
}
}
}
Java
복사
Remark
•
완전 탐색 문제
•
풀이 아이디어
◦
던전 배열과 최대 방문 수를 전역변수화
◦
방문 가능한 던전이 있으면 방문하는 재귀함수 사용
◦
더이상 방문이 가능한 던전이 없으면 for문을 탈출해 방문한 던전 수를 구한 후 최대치와 비교해서 더 크면 최대치로 등록
•
아래는 처음에 각 던전을 돈 후에 돌 수 있는 던전 수가 가장 많은 던전을 선택하는 그리디 알고리즘을 써서 틀린 풀이
◦
하지만 케이스가 8개로 경우의 수가 최대 8!개밖에 되지 않는 완전탐색 문제였음
import java.util.*;
class Solution {
public int solution(int k, int[][] dungeons) {
int answer = 0;
List<Dungeon> list = new ArrayList<>();
for (int[] dungeon : dungeons) {
list.add(new Dungeon(dungeon[0], dungeon[1]));
}
// 리스트가 0이 될 때까지 과정을 반복
while (list.size() > 0) {
Iterator<Dungeon> iter = list.iterator();
while (iter.hasNext()) {
Dungeon dungeon = iter.next();
if (k < dungeon.requiredHp) {
// 1. 피로도가 부족한 던전은 제거
iter.remove();
} else {
// 2. 각 던전을 탐험할 때 남는 피로도(remianHp)를 구함
dungeon.remainHp = k - dungeon.costHp;
}
}
if (list.size() == 0) break;
// 3. 각 던전 탐험 후 남는 피로도로 탐험할 수 있는 나머지 던전 수를 구함
for(int i = 0; i < list.size(); i++) {
list.get(i).next = 0;
for(int j = 0; j < list.size(); j++) {
if(i == j) continue;
if (list.get(i).remainHp >= list.get(j).requiredHp) {
list.get(i).next++;
}
}
}
// 4. next가 가장 큰 던전을 탐험하고 피로도를 소모
Dungeon dungeon = Collections.max(list, (o1, o2) -> o1.next - o2.next);
k -= dungeon.costHp;
list.remove(dungeon);
answer++;
}
return answer;
}
class Dungeon {
int requiredHp;
int costHp;
int remainHp;
int next;
Dungeon (int requiredHp, int costHp) {
this.requiredHp = requiredHp;
this.costHp = costHp;
}
}
}
Java
복사
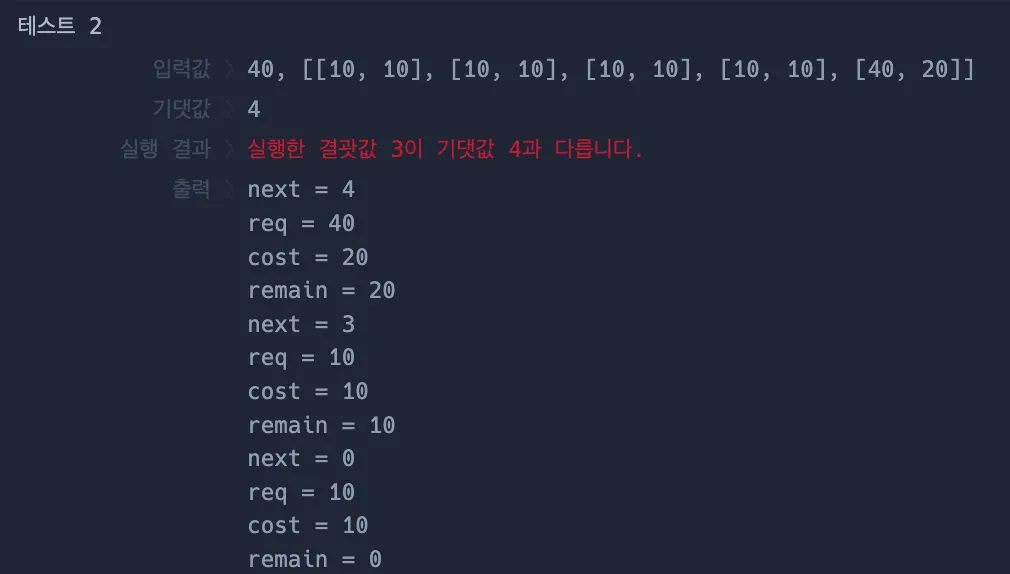
아래는 반례 케이스